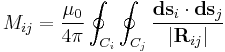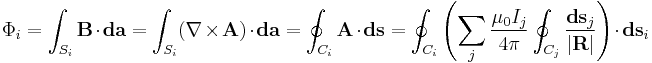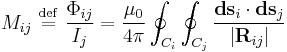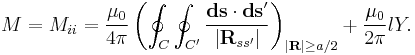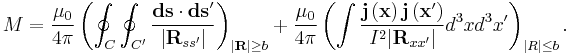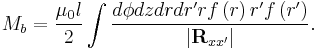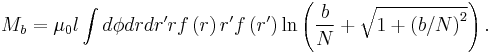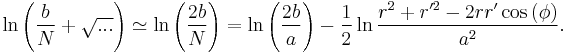Derivation of self inductance

The mutual inductance by circuit i on circuit j is given by the double integral Neumann formula

M_{ij} = \frac{\mu_0}{4\pi} \oint_{C_i}\oint_{C_j} \frac{\mathbf{ds}_i\cdot\mathbf{ds}_j}{|\mathbf{R}_{ij}|}

Contents

Derivation

\Phi_{i} = \int_{S_i} \mathbf{B}\cdot\mathbf{da} = \int_{S_i} (\nabla\times\mathbf{A})\cdot\mathbf{da} = \oint_{C_i} \mathbf{A}\cdot\mathbf{ds} = \oint_{C_i} \left(\sum_{j}\frac{\mu_0 I_j}{4\pi} \oint_{C_j} \frac{\mathbf{ds}_j}{|\mathbf{R}|}\right) \cdot \mathbf{ds}_i

where

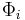\Phi_i\ \, is the magnetic flux through the ith surface by the electrical circuit outlined by Cj
Ci is the enclosing curve of Si.
B is the magnetic field vector.
A is the vector potential. [1]

Stokes' theorem has been used.

M_{ij} \ \stackrel{\mathrm{def}}{=}\ \frac{\Phi_{ij}}{I_j} = \frac{\mu_0}{4\pi} \oint_{C_i}\oint_{C_j} \frac{\mathbf{ds}_i\cdot\mathbf{ds}_j}{|\mathbf{R}_{ij}|}

so that the mutual inductance is a purely geometrical quantity independent of the current in the circuits.

Self inductance

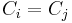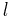In the self inductance case C_{i}=C_{j}. Therefore 1/R diverges and the finite radius of the wire and the distribution of the current in the wire must be taken into account. A generic formula for the self inductance M is available provided that the length l of the wire is much larger than its radius a :

M = M_{ii} = \frac{\mu_0}{4\pi} \left ( \oint_{C}\oint_{C'} \frac{\mathbf{ds}\cdot\mathbf{ds}'}{|\mathbf{R}_{ss^{\prime }}|}\right )_{|\mathbf{R}| \ge a/2} %2B \frac{\mu_0}{2\pi}lY.

Points with 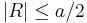|R|\leq a/2 now must be excluded in the curve integral. The correction term proportional to 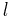l originates from short wire segments which are essentially cylinders. 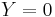Y=0 if the current flows in the surface of the wire, 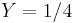Y=1/4 if the current is homogeneous in the wire.

For a derivation start from a slight generalization of the curve integral for mutual inductance,

M = \frac{\mu_0}{4\pi} \left( \oint_{C}\oint_{C'} \frac{\mathbf{ds}\cdot\mathbf{ds}'}{|\mathbf{R}_{ss^{\prime }}|}\right )_{|\mathbf{R}| \ge b} %2B \frac{\mu_0}{4\pi} \left( \int \frac{\mathbf{j}\left( \mathbf{x}\right)\mathbf{j}\left( \mathbf{x}^{\prime } \right)}{I^{2}|\mathbf{R}_{xx^{\prime }}|} d^{3}xd^{3}x^{\prime } \right )_{|R| \le b }.

Here j(x) is the current density, I is the total current, and b is a length according to 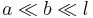a\ll b \ll l. The idea is to calculate the contribution from points with |R|> b with the curve integral, and to use the actual current density for the contribution 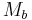M_{b} from points with |R|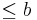\leq b. Let the current density in a wire segment be given by 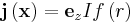\mathbf{j}\left( \mathbf{x }\right) =\mathbf{e}_{z}If\left( r\right), where r is a radial coordinate, and 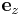\mathbf{e}_{z} is a unit vector along the axis. 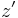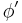Then, using cylinder coordinates and performing the trivial integrations over z' and \phi ^{\prime },

M_{b}=\frac{\mu _{0}l}{2}\int \frac{d\phi dzdrdr^{\prime }rf\left( r\right) r^{\prime }f\left( r^{\prime }\right) }{|\mathbf{R}_{xx^{\prime }}|}.

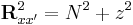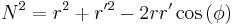The integral over z (from -b to b) may be performed using \mathbf{R}_{xx^{\prime }}^{2}=N^{2}%2Bz^{2}, N^{2}=r^{2}%2Br^{\prime 2}-2rr^{\prime }\cos \left( \phi \right),

M_{b}=\mu _{0}l\int d\phi drdr^{\prime }rf\left( r\right) r^{\prime }f\left( r^{\prime }\right) \ln \left( \frac{b}{N}%2B\sqrt{1%2B\left(b /N\right) ^{2}}\right) .

Because of N\ll b the logarithm may be replaced by

\ln \left( \frac{b}{N}%2B\sqrt{...}\right) \simeq \ln \left( \frac{ 2b }{N}\right) =\ln \left( \frac{2b}{a}\right) -\frac{1}{2}\ln \frac{r^{2}%2Br^{\prime 2}-2rr^{\prime }\cos \left( \phi \right) }{a^{2}}.

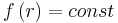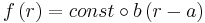In the realistic cases f\left( r\right)=const and f\left( r\right) =const\circ b \left( r-a\right) the remaining integrals now either are trivial or may be looked up in an integral table. The result is 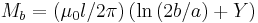M_{b}= \left( \mu _{0}l / 2\pi \right) \left( \ln \left( 2b /a\right) %2BY\right). Finally, the self inductance cannot depend on the arbitrary length b, which is the lower integration limit for the curve integral and the upper integration limit for 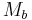M_{b}. Therefore the contribution proportional to 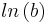ln\left(b \right) cancels against a contribution from the curve integral, so that one now also may choose 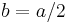b=a/2 to simplify the result.

Error estimation and restrictions

Wire segments of length b aren't perfect cylinders, they typically are curved by an angle 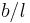b/l. The scalar product between current elements thus contains an additional factor of order 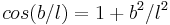cos(b/l)=1%2Bb^2/l^2. Endings of wire segments aren't perfectly parallel. The maximal length of such an ending is a, leading to a relative error a/b. A typical tilt angle only is b/l, leading to a factor 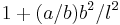1%2B(a/b)b^2/l^2. The curve integral uses distance along the axis instead of the distance between points anwhere in the wire. This contributes at most a factor 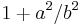1%2Ba^2/b^2. 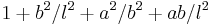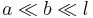In total, the expression is wrong by a factor 1%2Bb^2/l^2%2Ba^2/b^2%2Bab/l^2, which is small for a\ll b \ll l.

In the skin effect case another approximation is hidden in the assumption of constant current density. This may lead to wrong results because additional currents flow in the surface of wires close to each other (expelling the magnetic field). In this case the Laplace equation must be solved to determine currents and fields.

References

  1. ^ Jackson, J. D. (1975). Classical Electrodynamics. Wiley. pp. 176, 263.